Notes Chapter 9: Trigonometry II by Syakirah

Notes Chapter 8: Circles III by Syakirah

NOTES : Statistics III by Afrina

Notes Chapter 10: Angles of Elevation and Depression by Ambikai

http://www.youtube.com/watch?v=EJndVQiD9vM

History of the percent sign - by Yen Lin

HISTORY OF THE PERCENT SIGN

The percent sign (%) is the symbol used to indicate a percentage (that the preceding number is divided by one hundred).

Related signs include the permille (per thousand) sign ‰ and the permyriad (per ten thousand) sign ‱ (also known as a basis point), which indicate that a number is divided by one thousand or ten thousand respectively. Higher proportions use parts-per notation.

Evolution

Prior to 1425 there is no evidence of a special symbol being used for percentage. The Italian term per cento, "for a hundred", was used as well as several different abbreviations (e.g. "per 100", "p 100", "p cento", etc.). Examples of this can be seen in the 1339 arithmetic text depicted below.The letter p with its shaft crossed by a horizontal or diagonal strike conventionally stood for per, por, par, or pur in Medieval and Renaissance paleography.

At some point a scribe of some sort used the abbreviation "pc" with a tiny loop or circle (depicting the ending -o used in Italian numeration for primo, secondo,etc.) This appears in some additional pages of a 1425 text which were probably added around 1435. This is shown below.

The "pc" with a loop eventually evolved into a horizontal fraction sign by 1650 and thereafter lost the "per".

In 1925 D.E. Smith wrote, "The solidus form () is modern.

Probability Notes Chapter 7 by Afiqah Diyana.

history of circles by cynthia

                            Circles




The circle has been known since before the beginning of recorded history. Natural circles would have been observed, such as the Moon, Sun, and a short plant stalk blowing in the wind on sand, which forms a circle shape in the sand. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy, and calculus.
Early science, particularly geometry and astrology and astronomy, was connected to the divine for most medieval scholars, and many believed that there was something intrinsically "divine" or "perfect" that could be found in circles.






Some highlights in the history of the circle are:

• 1700 BCE – The Rhind papyrus gives a method to find the area of a circular field. The result corresponds to 256 / 81 (3.16049...) as an approximate value of π.^[1]
• 300 BCE – Book 3 of Euclid's Elements deals with the properties of circles.
• In Plato's Seventh Letter there is a detailed definition and explanation of the circle. Plato explains the perfect circle, and how it is different from any drawing, words, definition or explanation.
• 1880 CE– Lindemann proves that π is transcendental, effectively settling the millennia-old problem of squaring the circle.

MATHS INTERESTING FACTS

Maths Interesting Facts

• 
  

• What comes after a million, billion and trillion? A quadrillion, quintillion, sextillion, septillion, octillion, nonillion, decillion and undecillion.

• Different names for the number 0 include zero, nought, naught, nil, zilch and zip.

• Zero ( 0 ) is the only number which can not be represented by Roman numerals.

• The name 'zero' derives from the Arabic word sifr which also gave us the English word 'cipher' meaning 'a secret way of writing' .

• Do you know the magic of no. nine (9)? Multiply any number with nine (9 ) and then sum all individual digits of the result (product) to make it single digit, the sum of all these individual digits would always be nine (9).

• Here is an interesting trick to check divisibility of any number by number 3.A number is divisible by three if the sum of its digits is divisible by three (3).

• The = sign ("equals sign") was invented by 16th Century Welsh mathematician Robert Recorde, who was fed up with writing "is equal to" in his equations.

• Googol (meaning & origin of Google brand ) is the term used for a number 1 followed by 100 zeros and that it was used by a nine-year old, Milton Sirotta, in 1940.

• The name of the popular search engine ‘Google’ came from a misspelling of the word ‘googol’.

• Abacus is considered the origin of the calculator.

• Have you ever noticed that the opposite sides a die always add up to seven (7).

• Equal sign (=) was first used in 1557 by Robert Recorde, an Englishman.

• 12,345,678,987,654,321 is the product of 111,111,111 x 111,111,111. Notice the sequence of the numbers 1 to 9 and back to 1.

• Plus (+) and Minus (-) sign symbols were used as early as 1489 A.D.

• An icosagon is a shape with 20 sides.

• Trigonometry is the study of the relationship between the angles of triangles and their sides.

• If you add up the numbers 1-100 consecutively (1+2+3+4+5...) the total is 5050.

• 2 and 5 are the only primes that end in 2 or 5.

• From 0 to 1,000, the letter "A" only appears in 1,000 ("one thousand").

• A 'jiffy' is an actual unit of time for 1/100th of a second.

• 'FOUR' is the only number in the English language that is spelled with the same number of letters as the number itself

• 
  

The history of the Venn Diagram and John Venn by Sufie

Hello~

This post is about Venn Diagrams from Chapter 3

The history on John Venn:

John Venn FRS (4 August 1834 – 4 April 1923), was a British logician and philosopher. He is famous for introducing the Venn diagram, which is used in many fields, including set theory, probability, logic, statistics, and computer scienceVenn also had a rare skill in building machines. He used his skill to build a machine for bowling cricket balls, which was so good that when the Australian Cricket team visited Cambridge in 1909, Venn's machine clean bowled one of its top stars four times.

Venn's main area of interest was logic and he published three texts on the subject. He wrote The Logic of Chance which introduced the frequency interpretation or frequency theory of probability in 1866, Symbolic Logic which introduced the Venn diagrams in 1881, and The Principles of Empirical Logic in 1889.

In 1883, Venn was elected to the Royal Society. In 1897, he wrote a history of his college, called The Biographical History of Gonville and Caius College,1849–1897. He began a compilation of biographical notes of Cambridge University alumni, a work which was continued by his son, John Archibald Venn (1883–1958) and published as Alumni Cantabrigiensesin 10 volumes from 1922-1953.

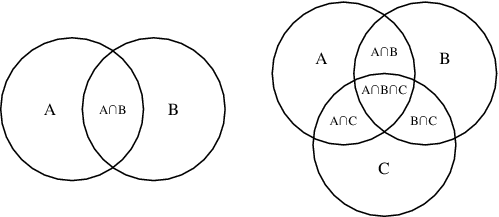
The Venn Diagram:

A Venn diagram is constructed with a collection of simple closed curves drawn in a plane. According to Lewis (1918), the "principle of these diagrams is that classes [or sets] be represented by regions in such relation to one another that all the possible logical relations of these classes can be indicated in the same diagram. That is, the diagram initially leaves room for any possible relation of the classes, and the actual or given relation, can then be specified by indicating that some particular region is null or is not-null".^[1]

Venn diagrams normally comprise overlapping circles. The interior of the circle symbolically represents the elements of the set, while the exterior represents elements that are not members of the set. For instance, in a two-set Venn diagram, one circle may represent the group of all wooden objects, while another circle may represent the set of all tables. The overlapping area or intersection would then represent the set of all wooden tables. Shapes other than circles can be employed as shown below by Venn's own higher set diagrams. Venn diagrams do not generally contain information on the relative or absolute sizes (cardinality) of sets; i.e. they are schematic diagrams.

Venn diagrams are similar to Euler diagrams. However, a Venn diagram for n component sets must contain all 2ⁿ hypothetically possible zones that correspond to some combination of inclusion or exclusion in each of the component sets. Euler diagrams contain only the actual possible zones for a particular given context. In Venn diagrams, a shaded zone may represent an empty zone, whereas in an Euler diagram the corresponding zone is missing from the diagram. For example, if one set represents dairy products and another cheeses, the Venn diagram contains a zone for cheeses that are not dairy products. Assuming that in the context cheese means some type of dairy product, the Euler diagram has the cheese zone entirely contained within the dairy-product zone—there is no zone for (non-existent) non-dairy cheese. This means that as the number of contours increases, Euler diagrams are typically less visually complex than the equivalent Venn diagram, particularly if the number of non-empty intersections is small.^[2]

-Yay for diagrams, Sufie

EXERCISES - CHAP 6

Chapter 6 exercises with answers! :D -Sarah Q-

Magic Maths Words by Andria

Math comics by Jazmeen

First comic




Second comic





Third comic





Forth comic




Fifth comic

Random stuff about Zero

Amrit's Brief History of Zero (from a random site)

From placeholder to the driver of calculus, zero has crossed the greatest minds and most diverse borders since it was born many centuries ago. Today, zero is perhaps the most pervasive global symbol known. In the story of zero, something can be made out of nothing.

Zero, zip, zilch - how often has a question been answered by one of these words? Countless, no doubt. Yet behind this seemingly simple answer conveying nothing lays the story of an idea that took many centuries to develop, many countries to cross, and many minds to comprehend. Understanding and working with zero is the basis of our world today; without zero we would lack calculus, financial accounting, the ability to make arithmetic computations quickly, and, especially in today's connected world, computers. The story of zero is the story of an idea that has aroused the imagination of great minds across the globe.

When anyone thinks of one hundred, two hundred, or seven thousand the image in his or her mind is of a digit followed by a few zeros. The zero functions as a placeholder; that is, three zeroes denotes that there are seven thousands, rather than only seven hundreds. If we were missing one zero, that would drastically change the amount. Just imagine having one zero erased (or added) to your salary! Yet, the number system we use today - Arabic, though it in fact came originally from India - is relatively new. For centuries people marked quantities with a variety of symbols and figures, although it was awkward to perform the simplest arithmetic calculations with these number systems.

The Sumerians were the first to develop a counting system to keep an account of their stock of goods - cattle, horses, and donkeys, for example. The Sumerian system was positional; that is, the placement of a particular symbol relative to others denoted its value. The Sumerian system was handed down to the Akkadians around 2500 BC and then to the Babylonians in 2000 BC. It was the Babylonians who first conceived of a mark to signify that a number was absent from a column; just as 0 in 1025 signifies that there are no hundreds in that number. Although zero's Babylonian ancestor was a good start, it would still be centuries before the symbol as we know it appeared.

The renowned mathematicians among the Ancient Greeks, who learned the fundamentals of their math from the Egyptians, did not have a name for zero, nor did their system feature a placeholder as did the Babylonian. They may have pondered it, but there is no conclusive evidence to say the symbol even existed in their language. It was the Indians who began to understand zero both as a symbol and as an idea.

Brahmagupta, around 650 AD, was the first to formalize arithmetic operations using zero. He used dots underneath numbers to indicate a zero. These dots were alternately referred to as 'sunya', which means empty, or 'kha', which means place. Brahmagupta wrote standard rules for reaching zero through addition and subtraction as well as the results of operations with zero. The only error in his rules was division by zero, which would have to wait for Isaac Newton and G.W. Leibniz to tackle.

But it would still be a few centuries before zero reached Europe. First, the great Arabian voyagers would bring the texts of Brahmagupta and his colleagues back from India along with spices and other exotic items. Zero reached Baghdad by 773 AD and would be developed in the Middle East by Arabian mathematicians who would base their numbers on the Indian system. In the ninth century, Mohammed ibn-Musa al-Khowarizmi was the first to work on equations that equaled zero, or algebra as it has come to be known. He also developed quick methods for multiplying and dividing numbers known as algorithms (a corruption of his name). Al-Khowarizmi called zero 'sifr', from which our cipher is derived. By 879 AD, zero was written almost as we now know it, an oval - but in this case smaller than the other numbers. And thanks to the conquest of Spain by the Moors, zero finally reached Europe; by the middle of the twelfth century, translations of Al-Khowarizmi's work had weaved their way to England.

The Italian mathematician, Fibonacci, built on Al-Khowarizmi's work with algorithms in his book Liber Abaci, or "Abacus book," in 1202. Until that time, the abacus had been the most prevalent tool to perform arithmetic operations. Fibonacci's developments quickly gained notice by Italian merchants and German bankers, especially the use of zero. Accountants knew their books were balanced when the positive and negative amounts of their assets and liabilities equaled zero. But governments were still suspicious of Arabic numerals because of the ease in which it was possible to change one symbol into another. Though outlawed, merchants continued to use zero in encrypted messages, thus the derivation of the word cipher, meaning code, from the Arabic sifr.

The next great mathematician to use zero was Rene Descartes, the founder of the Cartesian coordinate system. As anyone who has had to graph a triangle or a parabola knows, Descartes' origin is (0,0). Although zero was now becoming more common, the developers of calculus, Newton and Lebiniz, would make the final step in understanding zero.

Adding, subtracting, and multiplying by zero are relatively simple operations. But division by zero has confused even great minds. How many times does zero go into ten? Or, how many non-existent apples go into two apples? The answer is indeterminate, but working with this concept is the key to calculus. For example, when one drives to the store, the speed of the car is never constant - stoplights, traffic jams, and different speed limits all cause the car to speed up or slow down. But how would one find the speed of the car at one particular instant? This is where zero and calculus enter the picture.

If you wanted to know your speed at a particular instant, you would have to measure the change in speed that occurs over a set period of time. By making that set period smaller and smaller, you could reasonably estimate the speed at that instant. In effect, as you make the change in time approach zero, the ratio of the change in speed to the change in time becomes similar to some number over zero - the same problem that stumped Brahmagupta.

In the 1600's, Newton and Leibniz solved this problem independently and opened the world to tremendous possibilities. By working with numbers as they approach zero, calculus was born without which we wouldn't have physics, engineering, and many aspects of economics and finance.

In the twenty-first century zero is so familiar that to talk about it seems like much ado about nothing. But it is precisely understanding and working with this nothing that has allowed civilization to progress. The development of zero across continents, centuries, and minds has made it one of the greatest accomplishments of human society. Because math is a global language, and calculus its crowning achievement, zero exists and is used everywhere. But, like its function as a symbol and a concept meant to denote absence, zero may still seem like nothing at all. Yet, recall the fears over Y2K and zero no longer seems like a tale told by an idiot.

http://youtu.be/O6uoregIrX0

Chapter 2 Quadratic expressions and equation.
Kavisha (:

Maths history by ili rosli

It is believed that Ancient Egyptians used complex mathematics such as algebra, arithmetic and geometry as far back as 3000 BC, such as equations to approximate the area of circles. Babylonians measured the circumference of a circle as approximately 3 times the diameter, which is fairly close to today’s measurement which uses the value of Pi (around 3.14). Chinese mathematics developed around the 11th century BC and included important concepts related to negative numbers, decimals, algebra and geometry. Greek mathematics developed from around the 7th century BC, producing many important theories thanks to great mathematicians such as Pythagoras, Euclid and Archimedes. The Hindu-Arabic numeral system began developing as early as the 1st century with a full system being established around the 9th century, forming the basis of the numerical digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 that we use today. The symbols used for addition (+) and subtraction (-) have been around for thousands of years but it wasn't until the 16th century that most mathematical symbols were invented. Before this time math equations were written in words, making it very time consuming. The equals sign (=) was invented in 1557 by a Welsh mathematician named Robert Recorde. Mathematical developments increased rapidly around the time of the Italian Renaissance in the 16th century and continued through the scientific revolution of the 17th and 18th centuries, becoming increasingly abstract in the 19th and 20th centuries. The basic arithmetic operations used in mathematics are addition, subtraction, multiplication and division. Modern mathematics has advanced greatly thanks to the incredible computing power of today’s computers. These days mathematics is important in many different types of jobs, including those related to engineering, business, science and medicine :)

Maths Tricks

2's trick
Step1: Think of a number .
Step2: Multiply it by 3.
Step3: Add 6 with the getting result.
Step4: divide it by 3.
Step5: Subtract it from the first number used.

Answer: 2

Teach Me How To Factor (WSHS Math Rap Song)

Do The Quad Solve (WSHS Math Rap Song)

Math Song....memories :')

CHAPTER 4;  Mathematical Reasoning~

1. Mathematical Reasoning is a field of study regarding the methods and principles used to DIFFERENTIATE  between TRUE statements and  FALSE statements.
2. A statement is  sentence which is either true or false but NEVER BOTH.
3. ''ALL'' is a quantifiers implies  EVERY object or case that satisfies certains conditions. ''SOME'' is a quantifiers implies A FEW and not necessarily every object or case that satisfies certain conditions.
4. Negatiation is a process of changing a true statement to a false statement and nice versa by using the word ''NOT'' or ''NO''.
5. A truth table is used to evaluate the truth value of a compund sentence.
6. for two statements p and q, ''if p then q'' statement is an implication, where p is an ANTECEDENT and q is a CONSEQUENT.
7. An ARGUMENT is a process to make a conclusion based on given statements. the statements are called PREMISES. the premises and a conclusion form an argument.
8. An INDUCTION is a process to make a generalization conclusion based on specific cases.
9. A DEDUCTION is a process to make a generalization based on specific statement.

 just watch this video to understand better :)

http://www.youtube.com/watch?v=NXzGjH2x1gQ

Egyptians and their Mathematics

Civilisation reached a high level in Egypt at an early period. The country was well suited for the people, with a fertile land thanks to the river Nile yet with a pleasing climate. It was also a country which was easily defended having few natural neighbours to attack it for the surrounding deserts provided a natural barrier to invading forces. As a consequence Egypt enjoyed long periods of peace when society advanced rapidly.

By 3000 BC two earlier nations had joined to form a single Egyptian nation under a single ruler. Agriculture had been developed making heavy use of the regular wet and dry periods of the year. The Nile flooded during the rainy season providing fertile land which complex irrigation systems made fertile for growing crops. Knowing when the rainy season was about to arrive was vital and the study of astronomy developed to provide calendar information. The large area covered by the Egyptian nation required complex administration, a system of taxes, and armies had to be supported. As the society became more complex, records required to be kept, and computations done as the people bartered their goods. A need for counting arose, then writing and numerals were needed to record transactions.

By 3000 BC the Egyptians had already developed their hieroglyphic writing (egyptian numerals as well) . This marks the beginning of the Old Kingdom period during which the pyramids were built. For example the Great Pyramid at Giza was built around 2650 BC and it is a remarkable feat of engineering. This provides the clearest of indications that the society of that period had reached a high level of achievement.

Hieroglyphs for writing and counting gave way to a hieratic script for both writing and numerals. Here we are concerned with the arithmetical methods which they devised to work with these numerals

The Egyptian number systems were not well suited for arithmetical calculations. We are still today familiar with Roman numerals and so it is easy to understand that although addition of Roman numerals is quite satisfactory, multiplication and division are essentially impossible. The Egyptian system had similar drawbacks to that of Roman numerals. However, the Egyptians were very practical in their approach to mathematics and their trade required that they could deal in fractions. Trade also required multiplication and division to be possible so they devised remarkable methods to overcome the deficiencies in the number systems with which they had to work. Basically they had to devise methods of multiplication and division which only involved addition.

Early hieroglyphic numerals can be found on temples, stone monuments and vases. They give little knowledge about any mathematical calculations which might have been done with the number systems. While these hieroglyphs were being carved in stone there was no need to develop symbols which could be written more quickly. However, once the Egyptians began to use flattened sheets of the dried papyrus reed as "paper" and the tip of a reed as a "pen" there was reason to develop more rapid means of writing. This prompted the development of hieratic writing and numerals.

There must have been a large number of papyri, many dealing with mathematics in one form or another, but sadly since the material is rather fragile almost all have perished. It is remarkable that any have survived at all, and that they have is a consequence of the dry climatic conditions in Egypt. Two major mathematical documents survive.

The Rhind Papyrus

You can see an example of Egyptian mathematics written on the Rhind papyrus and another papyrus, the Moscow papyrus, with a translation into hieratic script. It is from these two documents that most of our knowledge of Egyptian mathematics comes and most of the mathematical information in this article is taken from ancient documents.   --------->

The Rhind papyrus is named after the Scottish Egyptologist A Henry Rhind, who purchased it in Luxor in 1858. The papyrus, a scroll about 6 metres long and ¹/₃ of a metre wide, was written around 1650 BC by the scribe Ahmes who states that he is copying a document which is 200 years older. The original papyrus on which the Rhind papyrus is based therefore dates from about 1850 BC.

Finally we examine some details of the ancient Egyptian calendar. As we mentioned above, it was important for the Egyptians to know when the Nile would flood and so this required calendar calculations. The beginning of the year was chosen as the heliacal rising of Sirius, the brightest star in the sky. The heliacal rising is the first appearance of the star after the period when it is too close to the sun to be seen. For Sirius this occurs in July and this was taken to be the start of the year. The Nile flooded shortly after this so it was a natural beginning for the year. The heliacal rising of Sirius would tell people to prepare for the floods. The year was computed to be 365 days long and this was certainly known by 2776 BC and this value was used for a civil calendar for recording dates. Later a more accurate value of 365 ¹/₄ days was worked out for the length of the year but the civil calendar was never changed to take this into account. In fact two calendars ran in parallel, the one which was used for practical purposes of sowing of crops, harvesting crops etc. being based on the lunar month. Eventually the civil year was divided into 12 months, with a 5 day extra period at the end of the year. The Egyptian calendar, although changed much over time, was the basis for the Julian and Gregorian calendars.

By : Wan Farra

Maths Notes - Quadratic Expressions and Equations ❤

CHAPTER 2!

Posted by: Afiqah Diyana Mohd Fadzli.

Math Jokes!

Mathematicians at the beach

Q : Why do you rarely find mathematicians spending time at the beach?
A : Because they have sine and cosine to get a tan and don't need the sun.

No homework

Pupil: Would you punish me for something I haven't done? 

Teacher: Of course not. 

Pupil: That's good because I haven't done my Math homework!

Powers 

Q : Why are powers like fish? 

A : Because they're all indices (in the seas!)

Sad Textbook

Q : Why did the Maths textbook look so sad? 

A : Because it had so many problems!

Hot corner

If it is cold, go and stand in the corner, because it is 90 degrees there.

                               BEST MATH JOKE EVER              

  Q :  Where does a cow stop to drink?                                                           

  A :  The milky wayyy!                                        AHAHAHAHAHAHAHAHA

~ PUI LIN 

http://www.youtube.com/watch?v=pRSwIvJVeME

-Chapter 5 Notes

-Ambikai -:)

Graphing Quadratic Functions - Example 1 (elisha Hosanna)

Chapter 1: Standard Form

What are significant figure? Significant figures are used to denote an exact value of numbers to acertain specific degree of accuracy . For example : 289 = 300 ( correct to 1 significant figure)

1.2 Standard Form : Used to express a very large or a very small in the form of  A X 10 whereby, A is larger than 1 but smaller than 10.

 *some texts missing*

~Elisha Hosanna

 

Beauty of Mathematics

Hey guys, i found the meaning of 101%!!!!

Beauty of Mathematics

-Andria

An App of Modern Maths..3..2..1

If you have ever wondered how mathematicians and mathematics have shaped the world we live in, this is the app for you. The Minds of Modern Mathematics takes you on an interactive journey that spans nearly 1,000 years. It tells the story of mathematics and how it has impacted almost every aspect of human progress, from science to music, art, architecture, and culture. 

Minds of Modern Mathematics is a digital recreation of a 50-foot-wide wall installation that was part of the groundbreaking 1961 Mathematica exhibition sponsored by IBM and designed by the legendary design team, Charles and Ray Eames. 

Composed with the same passion for design and interactive learning that fueled Charles and Ray Eames, the Minds of Modern Mathematics lets you explore the fascinating history of mathematics on your own terms. 

Minds of Modern Mathematics


By Andria Abdul Majid

Kid calls 911 for help with Maths

History of mathematics (video)

 By, Jazmeen Ravendran

history by cynthia

The history of Algebraic Expressions

The father of algebraic expressions

 

The Hellenistic mathematician Diophantus has traditionally been known as "the father of algebra but debate now exists as to whether or not Al-Khwarizmi deserves this title instead.^] Those who support Diophantus point to the fact that the algebra found in Al-Jabr is more elementary than the algebra found in Arithmetica and that Arithmetica is syncopated while Al-Jabr is fully rhetorical.^[77]

Those who support Al-Khwarizmi point to the fact that he gave an exhaustive explanation for the algebraic solution of quadratic equations with positive roots,^] and was the first to teach algebra in an elementary form and for its own sake, whereas Diophantus was primarily concerned with the theory of numbers. Al-Khwarizmi also introduced the fundamental concept of "reduction" and "balancing" (which he originally used the term al-jabr to refer to), referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation. Other supporters of Al-Khwarizmi point to his algebra no longer being concerned "with a series of problems to be resolved, but an exposition which starts with primitive terms in which the combinations must give all possible prototypes for equations, which hence forward explicitly constitute the true object of study. They also point to his treatment of an equation for its own sake and "in a generic manner, in sofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems. Al-Khwarizmi's work established algebra as a mathematical discipline that is independent of geometry and arithmetic

Algebra

Algebra is often referred to as a generalization of arithmetic: problems and operations are expressed in terms of variables as well as constants. A constant is some number that always has the same value, such as 3 or 14.89. A variable is a number that may have different values. In algebra, letters such as a, b, c, x, y, and z are often used to represent variables. In any given situation, a variable such as x may stand for one, two, or any number of values. For example, in the expression x + 5 = 7, the only value that x can have is 2. In the expression x² = 4, however, x can be either +2 or −2. And in the expression x + y = 9, x can have an unlimited number of values, depending on the value of y.

Origins of algebra

 

Algebra became popular as a way of expressing mathematical ideas in the early ninth century. Arab mathematician Al-Khwarizmi is credited with writing the first algebra book, Al-jabr waʾl Muqabalah, from which the English word algebra is derived. The title of the book translates as "restoring and balancing," which refers to the way in which equations are handled in algebra. Al-Khwarizmi's book was influential in its day and remained the most important text in algebra for many years.