http://youtu.be/O6uoregIrX0
Chapter 2 Quadratic expressions and equation.
Kavisha (:
Thursday, February 28, 2013
Wednesday, February 27, 2013
Maths history by ili rosli
It is believed that Ancient Egyptians used complex mathematics such as algebra, arithmetic and geometry as far back as 3000 BC, such as equations to approximate the area of circles.
Babylonians measured the circumference of a circle as approximately 3 times the diameter, which is fairly close to today’s measurement which uses the value of Pi (around 3.14).
Chinese mathematics developed around the 11th century BC and included important concepts related to negative numbers, decimals, algebra and geometry.
Greek mathematics developed from around the 7th century BC, producing many important theories thanks to great mathematicians such as Pythagoras, Euclid and Archimedes.
The Hindu-Arabic numeral system began developing as early as the 1st century with a full system being established around the 9th century, forming the basis of the numerical digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 that we use today.
The symbols used for addition (+) and subtraction (-) have been around for thousands of years but it wasn't until the 16th century that most mathematical symbols were invented. Before this time math equations were written in words, making it very time consuming.
The equals sign (=) was invented in 1557 by a Welsh mathematician named Robert Recorde.
Mathematical developments increased rapidly around the time of the Italian Renaissance in the 16th century and continued through the scientific revolution of the 17th and 18th centuries, becoming increasingly abstract in the 19th and 20th centuries.
The basic arithmetic operations used in mathematics are addition, subtraction, multiplication and division.
Modern mathematics has advanced greatly thanks to the incredible computing power of today’s computers.
These days mathematics is important in many different types of jobs, including those related to engineering, business, science and medicine :)
Maths Tricks
2's trick
Step1: Think of a number .
Step2: Multiply it by 3.
Step3: Add 6 with the getting result.
Step4: divide it by 3.
Step5: Subtract it from the first number used.
Step1: Think of a number .
Step2: Multiply it by 3.
Step3: Add 6 with the getting result.
Step4: divide it by 3.
Step5: Subtract it from the first number used.
Answer: 2
CHAPTER 4; Mathematical Reasoning~
- Mathematical Reasoning is a field of study regarding the methods and principles used to DIFFERENTIATE between TRUE statements and FALSE statements.
- A statement is sentence which is either true or false but NEVER BOTH.
- ''ALL'' is a quantifiers implies EVERY object or case that satisfies certains conditions. ''SOME'' is a quantifiers implies A FEW and not necessarily every object or case that satisfies certain conditions.
- Negatiation is a process of changing a true statement to a false statement and nice versa by using the word ''NOT'' or ''NO''.
- A truth table is used to evaluate the truth value of a compund sentence.
- for two statements p and q, ''if p then q'' statement is an implication, where p is an ANTECEDENT and q is a CONSEQUENT.
- An ARGUMENT is a process to make a conclusion based on given statements. the statements are called PREMISES. the premises and a conclusion form an argument.
- An INDUCTION is a process to make a generalization conclusion based on specific cases.
- A DEDUCTION is a process to make a generalization based on specific statement.
http://www.youtube.com/watch?v=NXzGjH2x1gQ
Egyptians and their Mathematics
Civilisation reached a high level in Egypt at an early period. The country was well suited for the people, with a fertile land thanks to the river Nile yet with a pleasing climate. It was also a country which was easily defended having few natural neighbours to attack it for the surrounding deserts provided a natural barrier to invading forces. As a consequence Egypt enjoyed long periods of peace when society advanced rapidly.
By 3000 BC two earlier nations had joined to form a single Egyptian nation under a single ruler. Agriculture had been developed making heavy use of the regular wet and dry periods of the year. The Nile flooded during the rainy season providing fertile land which complex irrigation systems made fertile for growing crops. Knowing when the rainy season was about to arrive was vital and the study of astronomy developed to provide calendar information. The large area covered by the Egyptian nation required complex administration, a system of taxes, and armies had to be supported. As the society became more complex, records required to be kept, and computations done as the people bartered their goods. A need for counting arose, then writing and numerals were needed to record transactions.
By 3000 BC the Egyptians had already developed their hieroglyphic writing (egyptian numerals as well) . This marks the beginning of the Old Kingdom period during which the pyramids were built. For example the Great Pyramid at Giza was built around 2650 BC and it is a remarkable feat of engineering. This provides the clearest of indications that the society of that period had reached a high level of achievement.
Hieroglyphs for writing and counting gave way to a hieratic script for both writing and numerals. Here we are concerned with the arithmetical methods which they devised to work with these numerals
The Egyptian number systems were not well suited for arithmetical calculations. We are still today familiar with Roman numerals and so it is easy to understand that although addition of Roman numerals is quite satisfactory, multiplication and division are essentially impossible. The Egyptian system had similar drawbacks to that of Roman numerals. However, the Egyptians were very practical in their approach to mathematics and their trade required that they could deal in fractions. Trade also required multiplication and division to be possible so they devised remarkable methods to overcome the deficiencies in the number systems with which they had to work. Basically they had to devise methods of multiplication and division which only involved addition.
Early hieroglyphic numerals can be found on temples, stone monuments and vases. They give little knowledge about any mathematical calculations which might have been done with the number systems. While these hieroglyphs were being carved in stone there was no need to develop symbols which could be written more quickly. However, once the Egyptians began to use flattened sheets of the dried papyrus reed as "paper" and the tip of a reed as a "pen" there was reason to develop more rapid means of writing. This prompted the development of hieratic writing and numerals.
There must have been a large number of papyri, many dealing with mathematics in one form or another, but sadly since the material is rather fragile almost all have perished. It is remarkable that any have survived at all, and that they have is a consequence of the dry climatic conditions in Egypt. Two major mathematical documents survive.
 |
| The Rhind Papyrus |
You can see an example of Egyptian mathematics written on the Rhind papyrus and another papyrus, the Moscow papyrus, with a translation into hieratic script. It is from these two documents that most of our knowledge of Egyptian mathematics comes and most of the mathematical information in this article is taken from ancient documents. --------->
The Rhind papyrus is named after the Scottish Egyptologist A Henry Rhind, who purchased it in Luxor in 1858. The papyrus, a scroll about 6 metres long and 1/3 of a metre wide, was written around 1650 BC by the scribe Ahmes who states that he is copying a document which is 200 years older. The original papyrus on which the Rhind papyrus is based therefore dates from about 1850 BC.
Finally we examine some details of the ancient Egyptian calendar. As we mentioned above, it was important for the Egyptians to know when the Nile would flood and so this required calendar calculations. The beginning of the year was chosen as the heliacal rising of Sirius, the brightest star in the sky. The heliacal rising is the first appearance of the star after the period when it is too close to the sun to be seen. For Sirius this occurs in July and this was taken to be the start of the year. The Nile flooded shortly after this so it was a natural beginning for the year. The heliacal rising of Sirius would tell people to prepare for the floods. The year was computed to be 365 days long and this was certainly known by 2776 BC and this value was used for a civil calendar for recording dates. Later a more accurate value of 365 1/4 days was worked out for the length of the year but the civil calendar was never changed to take this into account. In fact two calendars ran in parallel, the one which was used for practical purposes of sowing of crops, harvesting crops etc. being based on the lunar month. Eventually the civil year was divided into 12 months, with a 5 day extra period at the end of the year. The Egyptian calendar, although changed much over time, was the basis for the Julian and Gregorian calendars.
By : Wan Farra
Math Jokes!
Mathematicians at the beach
Q : Why do you rarely find mathematicians spending time at the beach?
A : Because they have sine and cosine to get a tan and don't need the sun.
A : Because they have sine and cosine to get a tan and don't need the sun.
No homework
Pupil: Would you punish me for something I haven't done?
Teacher: Of course not.
Pupil: That's good because I haven't done my Math homework!
Q : Why are powers like fish?
A : Because they're all indices (in the seas!)
Q : Why did the Maths textbook look so sad?
A : Because it had so many problems!
Hot corner
If it is cold, go and stand in the corner, because it is 90 degrees there.
BEST MATH JOKE EVER
Q : Where does a cow stop to drink?
A : The milky wayyy! AHAHAHAHAHAHAHAHA
~ PUI LIN
Chapter 1: Standard Form
What are significant figure? Significant figures are used to denote an exact value of numbers to acertain specific degree of accuracy . For example : 289 = 300 ( correct to 1 significant figure)
1.2 Standard Form : Used to express a very large or a very small in the form of A X 10 whereby, A is larger than 1 but smaller than 10.
~Elisha Hosanna
1.2 Standard Form : Used to express a very large or a very small in the form of A X 10 whereby, A is larger than 1 but smaller than 10.
*some texts missing*
~Elisha Hosanna
Tuesday, February 26, 2013
An App of Modern Maths..3..2..1
If you have ever wondered how mathematicians and mathematics have shaped the world we live in, this is the app for you. The Minds of Modern Mathematics takes you on an interactive journey that spans nearly 1,000 years. It tells the story of mathematics and how it has impacted almost every aspect of human progress, from science to music, art, architecture, and culture.
Minds of Modern Mathematics is a digital recreation of a 50-foot-wide wall installation that was part of the groundbreaking 1961 Mathematica exhibition sponsored by IBM and designed by the legendary design team, Charles and Ray Eames.
Composed with the same passion for design and interactive learning that fueled Charles and Ray Eames, the Minds of Modern Mathematics lets you explore the fascinating history of mathematics on your own terms.
Minds of Modern Mathematics
By Andria Abdul Majid
Minds of Modern Mathematics is a digital recreation of a 50-foot-wide wall installation that was part of the groundbreaking 1961 Mathematica exhibition sponsored by IBM and designed by the legendary design team, Charles and Ray Eames.
Composed with the same passion for design and interactive learning that fueled Charles and Ray Eames, the Minds of Modern Mathematics lets you explore the fascinating history of mathematics on your own terms.
Minds of Modern Mathematics
By Andria Abdul Majid
history by cynthia
The history of Algebraic Expressions
The father of algebraic expressions
The Hellenistic mathematician Diophantus has traditionally been known as "the father of algebra but debate now exists as to whether or not Al-Khwarizmi deserves this title instead.] Those who support Diophantus point to the fact that the algebra found in Al-Jabr is more elementary than the algebra found in Arithmetica and that Arithmetica is syncopated while Al-Jabr is fully rhetorical.[77]
Those who support Al-Khwarizmi point to the fact that he gave an exhaustive explanation for the algebraic solution of quadratic equations with positive roots,] and was the first to teach algebra in an elementary form and for its own sake, whereas Diophantus was primarily concerned with the theory of numbers. Al-Khwarizmi also introduced the fundamental concept of "reduction" and "balancing" (which he originally used the term al-jabr to refer to), referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation. Other supporters of Al-Khwarizmi point to his algebra no longer being concerned "with a series of problems to be resolved, but an exposition which starts with primitive terms in which the combinations must give all possible prototypes for equations, which hence forward explicitly constitute the true object of study. They also point to his treatment of an equation for its own sake and "in a generic manner, in sofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems. Al-Khwarizmi's work established algebra as a mathematical discipline that is independent of geometry and arithmetic
Algebra
Algebra is often referred to as a generalization of arithmetic:
problems and operations are expressed in terms of variables as well as
constants. A constant is some number that always has the same value, such as 3
or 14.89. A variable is a number that may have different values. In algebra,
letters such as a, b, c, x, y, and z are often used to represent variables. In
any given situation, a variable such as x may stand for one, two, or any number
of values. For example, in the expression x + 5 = 7, the only value that x can
have is 2. In the expression x2 = 4, however, x can be either +2 or −2.
And in the expression x + y = 9, x can have an unlimited number of values,
depending on the value of y.
Origins
of algebra
Algebra became popular
as a way of expressing mathematical ideas in the early ninth century. Arab
mathematician Al-Khwarizmi is credited with writing the first algebra book, Al-jabr
waʾl Muqabalah, from which the English word algebra is derived. The title
of the book translates as "restoring and balancing," which refers to
the way in which equations are handled in algebra. Al-Khwarizmi's book was
influential in its day and remained the most important text in algebra for many
years.
History time!
Let's learn about Pythagoras today~
Pythagoras of Samos (Ancient Greek: Πυθαγόρας ὁ Σάμιος [Πυθαγόρης in Ionian Greek] Pythagóras ho Sámios "Pythagoras the Samian", or simply Πυθαγόρας; b. about 570 – d. about 495 BC)[1][2] was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him. He was born on the island of Samos, and might have travelled widely in his youth, visiting Egyptand other places seeking knowledge. Around 530 BC, he moved to Croton, a Greek colony insouthern Italy, and there set up a religious sect. His followers pursued the religious rites and practices developed by Pythagoras, and studied his philosophical theories. The society took an active role in the politics of Croton, but this eventually led to their downfall. The Pythagorean meeting-places were burned, and Pythagoras was forced to flee the city. He is said to have ended his days in Metapontum.
Pythagorean theorem
Since the fourth century AD, Pythagoras has commonly been given credit for discovering thePythagorean theorem, a theorem in geometry that states that in a right-angled triangle the area of the square on the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares of the other two sides—that is, 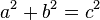 .
.
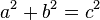 .
.
While the theorem that now bears his name was known and previously utilized by theBabylonians and Indians, he, or his students, are often said to have constructed the first proof. It must, however, be stressed that the way in which the Babylonians handled Pythagorean numbers implies that they knew that the principle was generally applicable, and knew some kind of proof, which has not yet been found in the (still largely unpublished) cuneiform sources.[46]Because of the secretive nature of his school and the custom of its students to attribute everything to their teacher, there is no evidence that Pythagoras himself worked on or proved this theorem. For that matter, there is no evidence that he worked on any mathematical or meta-mathematical problems. Some attribute it as a carefully constructed myth by followers of Platoover two centuries after the death of Pythagoras, mainly to bolster the case for Platonic meta-physics, which resonate well with the ideas they attributed to Pythagoras. This attribution has stuck down the centuries up to modern times.[47] The earliest known mention of Pythagoras's name in connection with the theorem occurred five centuries after his death, in the writings ofCicero and Plutarch.
-Yay for triangles, Sufie
HEY....here r some questions on chapter 1 by me (priya) :)
CHAPTER 1 : STANDARD FORM EXERCISE
1. Round off each of the following numbers to 3 significant
figures.
(a) 2963 = __________________
(b) 51852 = __________________
2. Round off 71.65 to
(a) 3 Significant figures = __________________
(b) 1 Significant figures = __________________
3. Round off
0.06053 to
(a) 3 Significant figures = __________________
(b) 2 Significant figures = __________________
(c) 1 Significant figures = __________________
4. Express each of the following numbers in standard form
(a) 48000 = ___________________
(b) 9200.05 = ___________________
(c) 0.026 = ___________________
(d) 0.00000038 = ___________________
5. Convert the following numbers in standard form to a
single number.
(a) 2.19×10^3 =
___________________
6. Evaluate each of the following and express your answers
in standard form.
(a) 16000000 + 2500000 = ____________________
(b) 0.69 + 10.451 =
____________________
7. Evaluate each of the following and express your answers
in standard form.
(a) 920000 – 87000 =
____________________
(b) 0.043 – 0.00095 =
____________________
10. Given that the mass of
a carbon atom and an oxygen
atom are 2 x 10^-23 g and 2.7 x 10^-23 respectively, one molecule of carbon dioxide gas
consist of one carbon atom and
two oxygen atoms. Calculate the mass in gram, of one molecule of carbon dioxide
gas.
Answer : _________________
By: Priyalini :D
Monday, February 25, 2013
Exercises!
Just to release your stress...
http://youtu.be/BRZZ4iZpLFk
Download:
http://adf.ly/1XjkgTopics:
Standard Form, Quadratic Expressions and Equations, Sets, Mathematical Reasoning, The Straight Line, Statistics, Probability I, Circles III, Angles of Elevation and Depression, and Lines and Planes in 3-Dimensions
Damia.
Maths exercises!
Hey people. Here are some exercises I found that we can try to do :-) http://adf.ly/1Xjkg, http://adf.ly/1WGNN. -Sarah Q
Subscribe to:
Comments (Atom)







