Wednesday, March 20, 2013
Notes Chapter 10: Angles of Elevation and Depression by Ambikai
Tuesday, March 19, 2013
History of the percent sign - by Yen Lin
HISTORY OF THE PERCENT SIGN
The percent sign (%) is the symbol used to indicate a percentage (that the preceding number is divided by one hundred).
Related signs include the permille (per thousand) sign ‰ and the permyriad (per ten thousand) sign ‱ (also known as a basis point), which indicate that a number is divided by one thousand or ten thousand respectively. Higher proportions use parts-per notation.
Evolution
Prior to 1425 there is no evidence of a special symbol being used for percentage. The Italian term per cento, "for a hundred", was used as well as several different abbreviations (e.g. "per 100", "p 100", "p cento", etc.). Examples of this can be seen in the 1339 arithmetic text depicted below.The letter p with its shaft crossed by a horizontal or diagonal strike conventionally stood for per, por, par, or pur in Medieval and Renaissance paleography.
At some point a scribe of some sort used the abbreviation "pc" with a tiny loop or circle (depicting the ending -o used in Italian numeration for primo, secondo,etc.) This appears in some additional pages of a 1425 text which were probably added around 1435. This is shown below.

The "pc" with a loop eventually evolved into a horizontal fraction sign by 1650 and thereafter lost the "per".


history of circles by cynthia
Circles
The circle has been known since before the beginning of recorded history. Natural circles would have been observed, such as the Moon, Sun, and a short plant stalk blowing in the wind on sand, which forms a circle shape in the sand. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy, and calculus.
Early science, particularly geometry and astrology and astronomy, was connected to the divine for most medieval scholars, and many believed that there was something intrinsically "divine" or "perfect" that could be found in circles.
Some highlights in the history of the circle are:
- 1700 BCE – The Rhind papyrus gives a method to find the area of a circular field. The result corresponds to 256 / 81 (3.16049...) as an approximate value of π.[1]
- 300 BCE – Book 3 of Euclid's Elements deals with the properties of circles.
- In Plato's Seventh Letter there is a detailed definition and explanation of the circle. Plato explains the perfect circle, and how it is different from any drawing, words, definition or explanation.
- 1880 CE– Lindemann proves that π is transcendental, effectively settling the millennia-old problem of squaring the circle.

MATHS INTERESTING FACTS
Maths Interesting Facts
- What comes after a million, billion and trillion? A quadrillion, quintillion, sextillion, septillion, octillion, nonillion, decillion and undecillion.
- Different names for the number 0 include zero, nought, naught, nil, zilch and zip.
- Zero ( 0 ) is the only number which can not be represented by Roman numerals.
- The name 'zero' derives from the Arabic word sifr which also gave us the English word 'cipher' meaning 'a secret way of writing' .
- Do you know the magic of no. nine (9)? Multiply any number with nine (9 ) and then sum all individual digits of the result (product) to make it single digit, the sum of all these individual digits would always be nine (9).
- Here is an interesting trick to check divisibility of any number by number 3.A number is divisible by three if the sum of its digits is divisible by three (3).
- The = sign ("equals sign") was invented by 16th Century Welsh mathematician Robert Recorde, who was fed up with writing "is equal to" in his equations.
- Googol (meaning & origin of Google brand ) is the term used for a number 1 followed by 100 zeros and that it was used by a nine-year old, Milton Sirotta, in 1940.
- The name of the popular search engine ‘Google’ came from a misspelling of the word ‘googol’.
- Abacus is considered the origin of the calculator.
- Have you ever noticed that the opposite sides a die always add up to seven (7).
- Equal sign (=) was first used in 1557 by Robert Recorde, an Englishman.
- 12,345,678,987,654,321 is the product of 111,111,111 x 111,111,111. Notice the sequence of the numbers 1 to 9 and back to 1.
- Plus (+) and Minus (-) sign symbols were used as early as 1489 A.D.
- An icosagon is a shape with 20 sides.
- Trigonometry is the study of the relationship between the angles of triangles and their sides.
- If you add up the numbers 1-100 consecutively (1+2+3+4+5...) the total is 5050.
- 2 and 5 are the only primes that end in 2 or 5.
- From 0 to 1,000, the letter "A" only appears in 1,000 ("one thousand").
- A 'jiffy' is an actual unit of time for 1/100th of a second.
- 'FOUR' is the only number in the English language that is spelled with the same number of letters as the number itself
Monday, March 18, 2013
The history of the Venn Diagram and John Venn by Sufie
Hello~
This post is about Venn Diagrams from Chapter 3
The history on John Venn:
John Venn FRS (4 August 1834 – 4 April 1923), was a British logician and philosopher. He is famous for introducing the Venn diagram, which is used in many fields, including set theory, probability, logic, statistics, and computer scienceVenn also had a rare skill in building machines. He used his skill to build a machine for bowling cricket balls, which was so good that when the Australian Cricket team visited Cambridge in 1909, Venn's machine clean bowled one of its top stars four times.
Venn's main area of interest was logic and he published three texts on the subject. He wrote The Logic of Chance which introduced the frequency interpretation or frequency theory of probability in 1866, Symbolic Logic which introduced the Venn diagrams in 1881, and The Principles of Empirical Logic in 1889.
In 1883, Venn was elected to the Royal Society. In 1897, he wrote a history of his college, called The Biographical History of Gonville and Caius College,1849–1897. He began a compilation of biographical notes of Cambridge University alumni, a work which was continued by his son, John Archibald Venn (1883–1958) and published as Alumni Cantabrigiensesin 10 volumes from 1922-1953.
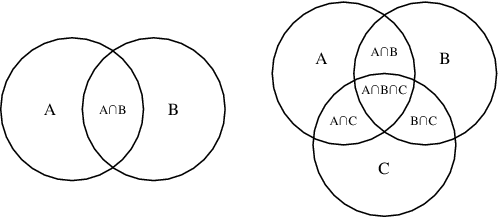
The Venn Diagram:
A Venn diagram is constructed with a collection of simple closed curves drawn in a plane. According to Lewis (1918), the "principle of these diagrams is that classes [or sets] be represented by regions in such relation to one another that all the possible logical relations of these classes can be indicated in the same diagram. That is, the diagram initially leaves room for any possible relation of the classes, and the actual or given relation, can then be specified by indicating that some particular region is null or is not-null".[1]
Venn diagrams normally comprise overlapping circles. The interior of the circle symbolically represents the elements of the set, while the exterior represents elements that are not members of the set. For instance, in a two-set Venn diagram, one circle may represent the group of all wooden objects, while another circle may represent the set of all tables. The overlapping area or intersection would then represent the set of all wooden tables. Shapes other than circles can be employed as shown below by Venn's own higher set diagrams. Venn diagrams do not generally contain information on the relative or absolute sizes (cardinality) of sets; i.e. they are schematic diagrams.
Venn diagrams are similar to Euler diagrams. However, a Venn diagram for n component sets must contain all 2n hypothetically possible zones that correspond to some combination of inclusion or exclusion in each of the component sets. Euler diagrams contain only the actual possible zones for a particular given context. In Venn diagrams, a shaded zone may represent an empty zone, whereas in an Euler diagram the corresponding zone is missing from the diagram. For example, if one set represents dairy products and another cheeses, the Venn diagram contains a zone for cheeses that are not dairy products. Assuming that in the context cheese means some type of dairy product, the Euler diagram has the cheese zone entirely contained within the dairy-product zone—there is no zone for (non-existent) non-dairy cheese. This means that as the number of contours increases, Euler diagrams are typically less visually complex than the equivalent Venn diagram, particularly if the number of non-empty intersections is small.[2]
-Yay for diagrams, Sufie
Sunday, March 17, 2013
Monday, March 4, 2013
Random stuff about Zero
Amrit's Brief History of Zero (from a random site)
From placeholder to the driver of calculus, zero has crossed the greatest minds and most diverse borders since it was born many centuries ago. Today, zero is perhaps the most pervasive global symbol known. In the story of zero, something can be made out of nothing.
Zero, zip, zilch - how often has a question been answered by one of these words? Countless, no doubt. Yet behind this seemingly simple answer conveying nothing lays the story of an idea that took many centuries to develop, many countries to cross, and many minds to comprehend. Understanding and working with zero is the basis of our world today; without zero we would lack calculus, financial accounting, the ability to make arithmetic computations quickly, and, especially in today's connected world, computers. The story of zero is the story of an idea that has aroused the imagination of great minds across the globe.
When anyone thinks of one hundred, two hundred, or seven thousand the image in his or her mind is of a digit followed by a few zeros. The zero functions as a placeholder; that is, three zeroes denotes that there are seven thousands, rather than only seven hundreds. If we were missing one zero, that would drastically change the amount. Just imagine having one zero erased (or added) to your salary! Yet, the number system we use today - Arabic, though it in fact came originally from India - is relatively new. For centuries people marked quantities with a variety of symbols and figures, although it was awkward to perform the simplest arithmetic calculations with these number systems.
The Sumerians were the first to develop a counting system to keep an account of their stock of goods - cattle, horses, and donkeys, for example. The Sumerian system was positional; that is, the placement of a particular symbol relative to others denoted its value. The Sumerian system was handed down to the Akkadians around 2500 BC and then to the Babylonians in 2000 BC. It was the Babylonians who first conceived of a mark to signify that a number was absent from a column; just as 0 in 1025 signifies that there are no hundreds in that number. Although zero's Babylonian ancestor was a good start, it would still be centuries before the symbol as we know it appeared.
The renowned mathematicians among the Ancient Greeks, who learned the fundamentals of their math from the Egyptians, did not have a name for zero, nor did their system feature a placeholder as did the Babylonian. They may have pondered it, but there is no conclusive evidence to say the symbol even existed in their language. It was the Indians who began to understand zero both as a symbol and as an idea.
Brahmagupta, around 650 AD, was the first to formalize arithmetic operations using zero. He used dots underneath numbers to indicate a zero. These dots were alternately referred to as 'sunya', which means empty, or 'kha', which means place. Brahmagupta wrote standard rules for reaching zero through addition and subtraction as well as the results of operations with zero. The only error in his rules was division by zero, which would have to wait for Isaac Newton and G.W. Leibniz to tackle.
But it would still be a few centuries before zero reached Europe. First, the great Arabian voyagers would bring the texts of Brahmagupta and his colleagues back from India along with spices and other exotic items. Zero reached Baghdad by 773 AD and would be developed in the Middle East by Arabian mathematicians who would base their numbers on the Indian system. In the ninth century, Mohammed ibn-Musa al-Khowarizmi was the first to work on equations that equaled zero, or algebra as it has come to be known. He also developed quick methods for multiplying and dividing numbers known as algorithms (a corruption of his name). Al-Khowarizmi called zero 'sifr', from which our cipher is derived. By 879 AD, zero was written almost as we now know it, an oval - but in this case smaller than the other numbers. And thanks to the conquest of Spain by the Moors, zero finally reached Europe; by the middle of the twelfth century, translations of Al-Khowarizmi's work had weaved their way to England.
The Italian mathematician, Fibonacci, built on Al-Khowarizmi's work with algorithms in his book Liber Abaci, or "Abacus book," in 1202. Until that time, the abacus had been the most prevalent tool to perform arithmetic operations. Fibonacci's developments quickly gained notice by Italian merchants and German bankers, especially the use of zero. Accountants knew their books were balanced when the positive and negative amounts of their assets and liabilities equaled zero. But governments were still suspicious of Arabic numerals because of the ease in which it was possible to change one symbol into another. Though outlawed, merchants continued to use zero in encrypted messages, thus the derivation of the word cipher, meaning code, from the Arabic sifr.
The next great mathematician to use zero was Rene Descartes, the founder of the Cartesian coordinate system. As anyone who has had to graph a triangle or a parabola knows, Descartes' origin is (0,0). Although zero was now becoming more common, the developers of calculus, Newton and Lebiniz, would make the final step in understanding zero.
Adding, subtracting, and multiplying by zero are relatively simple operations. But division by zero has confused even great minds. How many times does zero go into ten? Or, how many non-existent apples go into two apples? The answer is indeterminate, but working with this concept is the key to calculus. For example, when one drives to the store, the speed of the car is never constant - stoplights, traffic jams, and different speed limits all cause the car to speed up or slow down. But how would one find the speed of the car at one particular instant? This is where zero and calculus enter the picture.
If you wanted to know your speed at a particular instant, you would have to measure the change in speed that occurs over a set period of time. By making that set period smaller and smaller, you could reasonably estimate the speed at that instant. In effect, as you make the change in time approach zero, the ratio of the change in speed to the change in time becomes similar to some number over zero - the same problem that stumped Brahmagupta.
In the 1600's, Newton and Leibniz solved this problem independently and opened the world to tremendous possibilities. By working with numbers as they approach zero, calculus was born without which we wouldn't have physics, engineering, and many aspects of economics and finance.
In the twenty-first century zero is so familiar that to talk about it seems like much ado about nothing. But it is precisely understanding and working with this nothing that has allowed civilization to progress. The development of zero across continents, centuries, and minds has made it one of the greatest accomplishments of human society. Because math is a global language, and calculus its crowning achievement, zero exists and is used everywhere. But, like its function as a symbol and a concept meant to denote absence, zero may still seem like nothing at all. Yet, recall the fears over Y2K and zero no longer seems like a tale told by an idiot.
Subscribe to:
Comments (Atom)